Please contact me if you are interested in any of the research directions below. |
|
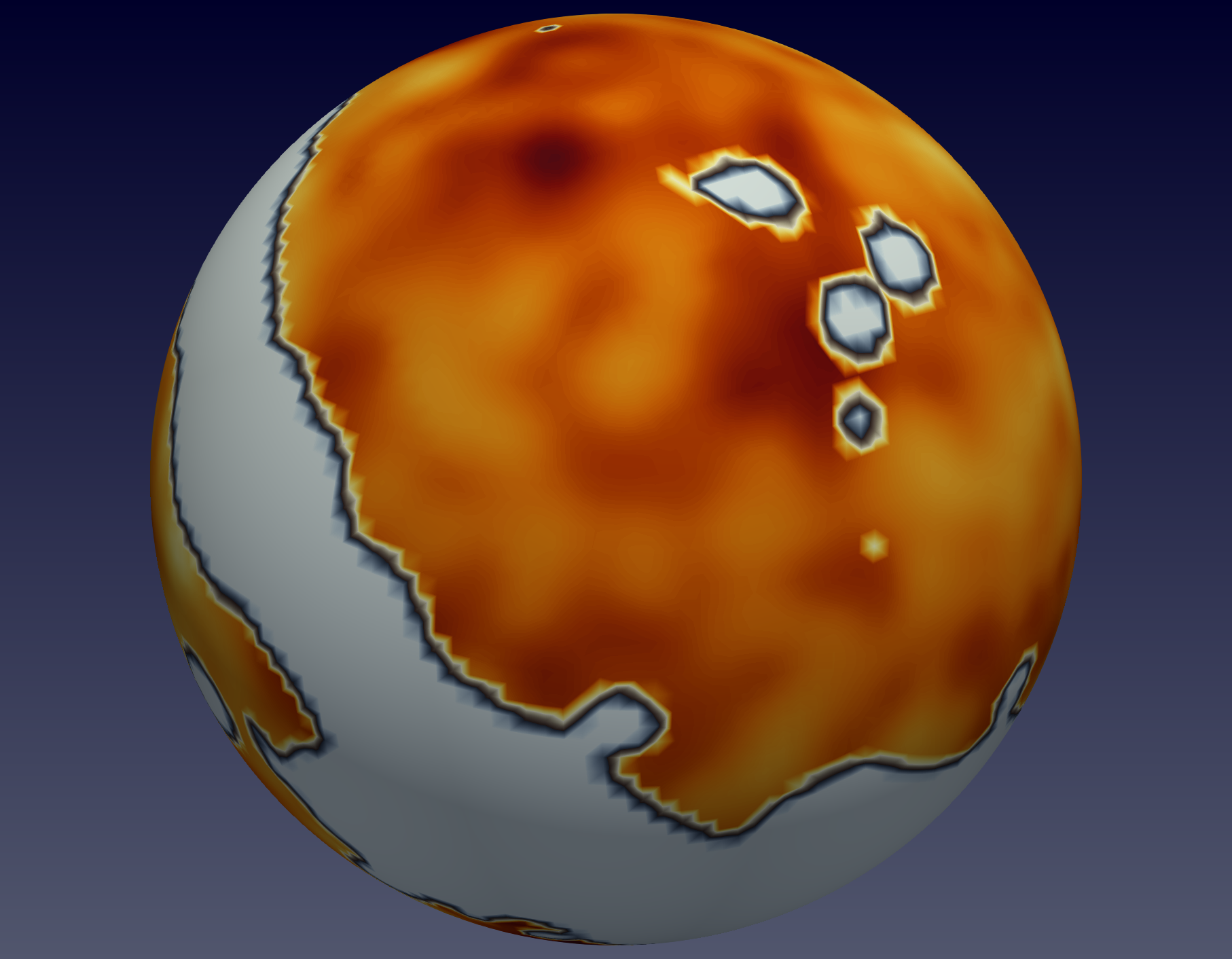 |
Cosmic Microwave Background
Cosmic Microwave Background (CMB) radiation is emitted at the epoch of recombination, when mater and radiation separate. The CMB represents the largest canvas on which to test the assumptions of the standard cosmological model, namely statistical homogeneity, isotropy and Gaussianity. The temperature fluctuations in the CMB are linked to the fluctuations in the stochastic matter field, thus studying the CMB field has the potential to shed light on the mechanisms in the infant Universe, as well as the nature of the primordial matter distribution field. I am interested in investigating the topo-geometrical characteristics of the CMB field with a view to gain a better understanding in the aforementioned directions.
|
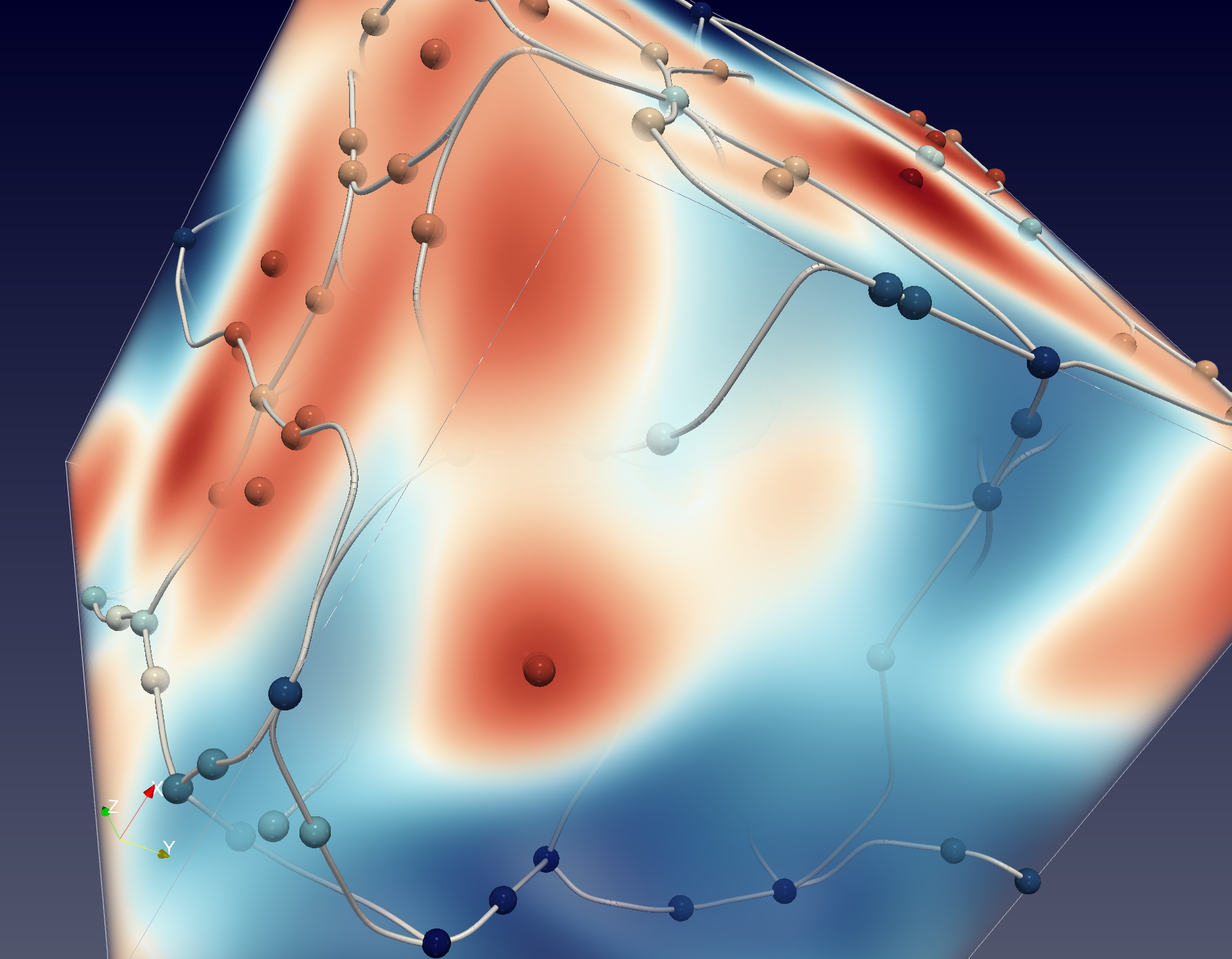 |
Gaussian random fields
Gaussian random fields model a variety of phenomena in the real world. Most famously, Gaussian random fields serve as the null hypothesis model for the primordial stochastic matter distribution. In view of this, I investigate the topo-geometrical properties of Gaussian random fields to establish a reference baseline.
|
 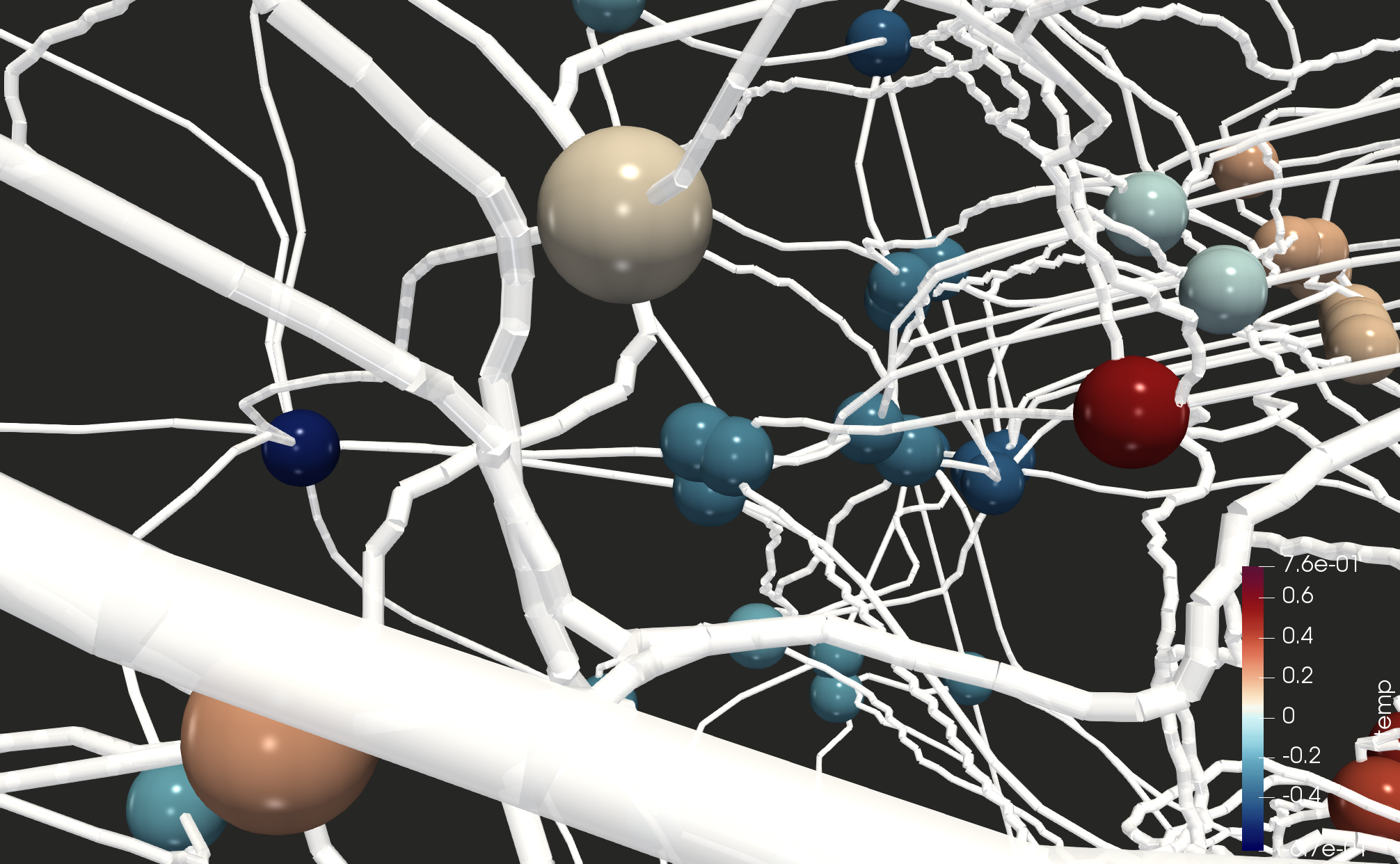 |
Large Scale structure of the Universe
At very large scales spanning millions of light years, the universe has a web-like appearance, commonly known as the cosmic web, composed of huge, roughly spherical blobs called clusters, connected by gigantic tenuous tentacles, known as filaments, woven around quasi 2D walls, which surround vast near-empty cosmic voids. The structural patterns of the cosmic web are imprinted with subtle information about the nature of dark matter and dark energy. Characterising the components of the cosmic web is also important for understanding the impact of the large scale environment on the formation and evolution of galaxies. I focus on developing a description of the components of the cosmic web, as well as topological characterisation of the connectivity properties, to facilitate a better understanding of the aforementioned challenges.
|
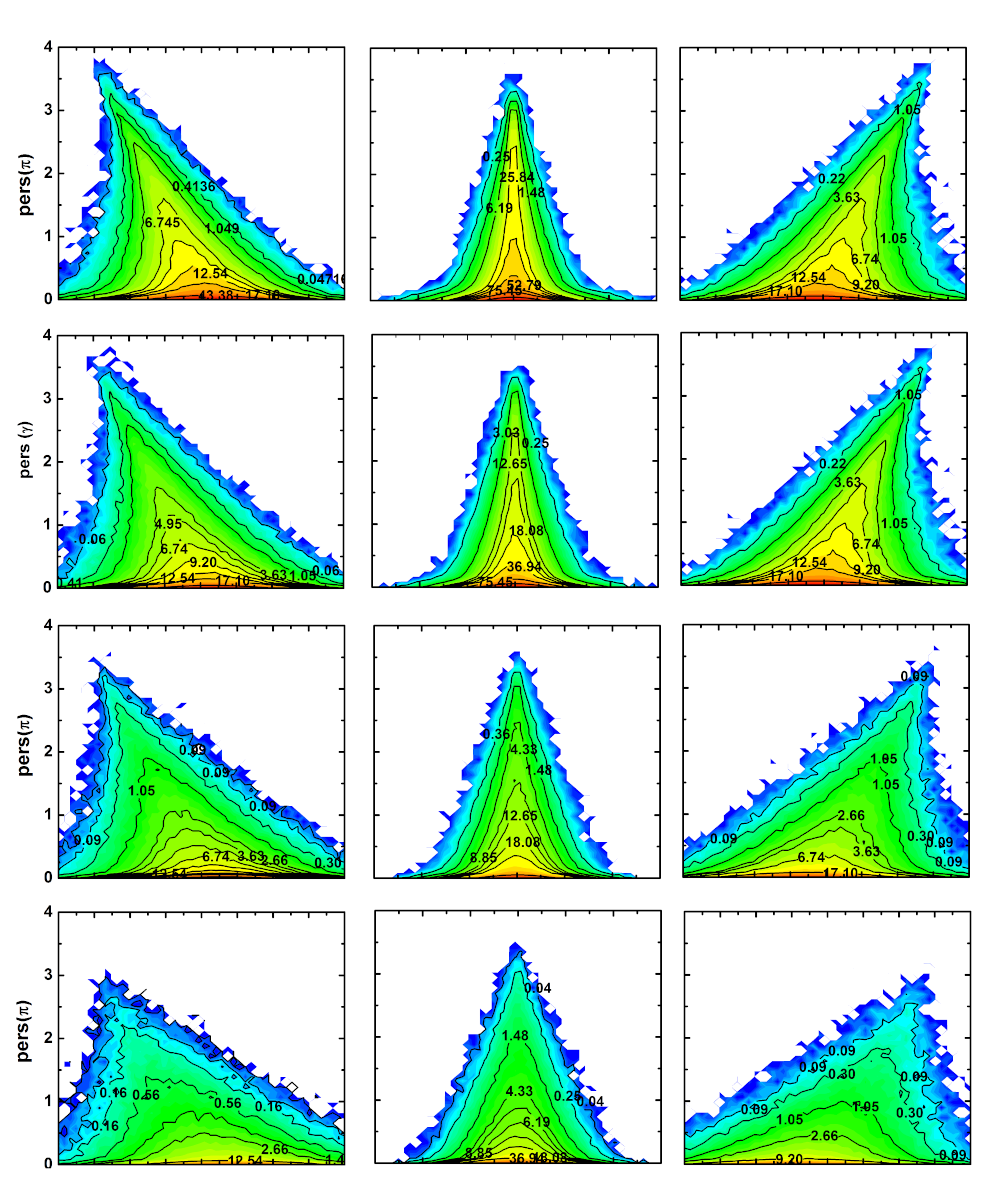 |
Stochastic topology
Persistence diagrams are the mainstay of topological data analysis. They encode the topological changes of evolving levelsets of a manifold in entirety, however gleaning meaningful information out of them is not entirely easy. As a part of my research, I focus on understanding the properties of persistence diagrams of stochastic processes.
|
 |
Persistent Holes in the Universe: A (hierarchical topology of the cosmic mass distribution
Pratyush Pranav. Ph.D. thesis. Kapteyn Astronomical Institute, University of Groningen. [Official link] Over scales of millions of light years, the Universe is a filigree of interconnected components of various dimensions and scales. This connected pattern, known as the Cosmic Web, consists of galaxies, intergalactic gas, and dark matter that have aggregated in an intricate wispy spatial pattern marked by dense compact clusters, elongated filaments and sheet-like walls, surrounding large near-empty void regions. A distinct feature of the Cosmic web is its intrinsic hierarchical arrangement, within which the elements of the web are ubiquitous at all density ranges and scales.
The patterns in the web have significant implications for the understanding of the growth of structures in the Universe, as well as for the understanding of formation and evolution of galaxies. As a result, the efforts to characterise the Cosmic Web has been an ongoing effort for decades now, developing and employing a range of techniques and tools, broadly based on statistical, geometric and topological concepts. This thesis concentrates on the description and detection of patterns in the Cosmic Web by harnessing the recent state-of-art techniques developed in the field of topology, involving Homology, Persistence and Morse theory. These techniques are capable of expressing topology in a greater detail compared to traditional descriptors like Euler characteristic and Minkowski functionals. Additionally, persistence describes topology in a hierarchical fashion, which ties in to the hierarchical characteristics of the web. Based on these techniques, this thesis also presents a visualization and analysis software to detect and quantify the filamentary patterns of the Cosmic Web. |

I aim to understand the formation, evolution and characteristics of structure in the Universe via topo-geometrical methods. Simultaneously, cosmological problems present an ideal setting for developing new, and refining existing topo-geometrical methodologies. This cross-disciplinary interaction is at the core of my research interests.